Qualität bedeutet, dass eine Arbeit ihren Verwendungszweck erfüllen muss. Wer Veränderliche beobachtet, möchte seine Beobachtungen sicher nicht nur im Schrank archivieren, sondern möchte sie der Öffentlichkeit zugänglich  machen. Das heißt aber, dass er sie so aufbereiten muss, dass sie den Ansprüchen der Öffentlichkeit genügen. Die  Öffentlichkeit besteht in diesem Fall häufig aus Fachastronomen, die Amateur- und eigene Beobachtungen für ihre Arbeiten verwenden. Amateure müssen also den Bedingungen genügen, die Fachastronomen stellen. Sie müssen sich schon vor Beginn ihrer Beobachtung darüber klar werden, wie sie den Qualitätsansprüchen der Fachwelt genügen können.

Qualitätssicherung umfasst in diesem Fall

• • Planung                    
  • Ausführung                    
  • Auswertung                    
  • Berichterstattung                    

einer Beobachtung bzw. einer Beobachtungsnacht.

Zur PLANUNG gehört, dass man sich auf die Beobachtungsnacht vorbereitet. Dass man das Bier, das man gerade trinken wollte, wieder in den Kühlschrank zurückstellt,  dass Umgebungskarten bereitliegen, dass die Uhr kontrolliert wird, auch ein Blick auf den Kalender kann nicht schaden usw.

Zur AUSFÜHRUNG gehört, dass man sich mit dem Umfeld des Veränderlichen vertraut macht, dass man entspannt schätzt, dass man für CCD-Aufnahmen den richtigen Filter und die richtige Belichtungszeit wählt, um ein gutes Signal-Rausch-Verhältnis zu erzielen usw.

Für die AUSWERTUNG sind die besten vorhandenen Mittel, Rechenverfahren, Fotometrieprogramme usw. zu wählen und man sollte die Ergebnisse auf Plausibilität prüfen und im Zweifel zurückhalten, bis sie bestätigt sind.

Die BERICHTERSTATTUNG schließlich soll die erzielten Ergebnisse einem Leserkreis verständlich machen.

Wir alle wollen genau beobachten. Was aber verbirgt sich hinter diesem Begriff? Stellen Sie sich auf einem Schützenfest verschiedene Trefferbilder auf der Scheibe vor: Die vier Bilder der folgenden Abbildung sollen veranschaulichen,  dass es sowohl auf die Streuung der Treffer (Präzision, Precision) als auch auf die Lage zum Ziel (Akkuratesse, Accuracy) ankommt.

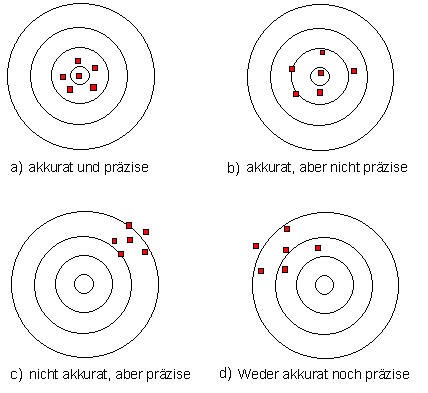
Abb. 1: Vier Trefferbilder beim Schützenfest veranschaulichen die Fehlerarten.

Schütze a) hat eine ruhige Hand bewiesen in der ein gut justiertes Gewehr lag.

Schütze b) hat im Mittel  zwar gut getroffen, aber vermutlich hat seine Hand gezittert. 

Schütze c) hat ein gutes Gewehr, aber er hat geschielt oder sein Zielfernrohr war nicht richtig justiert.

Schütze d) schließlich war wohl zu aufgeregt, um präzise zu schießen und sein Gewehr war wohl auch nicht gepflegt.

Zwei Arten von Fehlern beeinflussen Akkuratesse und Präzision:  Systematische und zufällige Fehler.

SYSTEMATISCHE FEHLER (z. B. Fälle c), d)) beeinflussen die Messung in  bestimmter, nicht immer bekannter Richtung. Oft erkennt man sie erst beim Vergleich unterschiedlicher Messungen derselben Größe.

Beispiele:                     

• • Falscher Gang der Uhr, Zeitumstellung nicht beachtet                     
  • Dark- oder Flat nicht angebracht                     
  • Falsches Filter im Strahlengang                     
  • Falscher Vergleichsstern verwendet                     
  • Voreingenommenheit beim Schätzen                     

ZUFÄLLIGE FEHLER (z. B. Fälle b), d)) sind Fehler, die infolge störender Einflüsse und wegen der Unzulänglichkeit der subjektiven Beobachtung zufällige Abweichungen vom wahren Wert mit sich bringen.

 Beispiele:                     

• • Händezittern beim Schießen                     
  • Streuung der Extinktion in Wolkenlücken                     
  • Statistische Schwankungen des Photonenflusses                     
  • Digitalisierungsfehler (Rundungsfehler)                     

Die Fehlertheorie gibt uns Formeln in die Hand, mit denen wir zufällige Fehler abschätzen können. Voraussetzung ist, dass wir genügend viele Messungen haben, so dass die Regeln der Statistik angewendet werden können und dass die Messungen unabhängig voneinander sind, d. h. dass sie sich nicht gegenseitig beeinflussen. Trägt man die Messwerte xi entsprechend ihrer Häufigkeit auf, erhält man die Gauss'sche Glockenkurve.

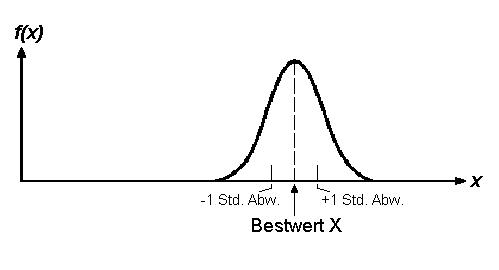
Daraus lassen sich ableiten:

Bestwert X = arithmetisches Mittel:   

Varianz = sigma²:

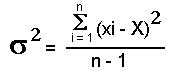
Standardabweichung = mittlerer Fehler der Einzelmessung:

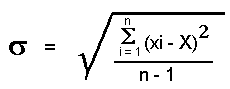
Mittlerer Fehler des Mittelwerts:

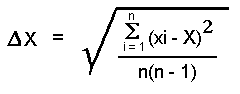
Zum Schluß einige Merksätze und Faustregeln die dem mit Statistik nicht vertrauten Beobachter das Leben erleichtern sollen:

• • Varianz und Standardabweichung sind unabhängig von der Zahl der Messwerte.                    
  • Der Fehler des Mittelwerts verringert sich proportional zu 1/WURZEL(n), d. h. Nachlässigkeit beim Messen rächt sich quadratisch.                    
  • Die Mathematik zeigt, dass 99,7 % aller Messwerte innerhalb  ±3 sigma liegen. Daraus folgt als Abschätzung für die Standardabweichung: sigma ~ Bandbreite der Messungen / 6 oder mit Sicherheitsmarge: sigma ~ Bandbreite / 5.                     
  • Checklisten sind probate Mittel, um auch in der Hektik nichts zu vergessen.                    
  • An Regeln, die man sich selber gibt, muss man sich auch halten.

Literatur:

EHRENBERG A. S. C.: Statistik oder der Umgang mit Daten, 
			VCH Verlagsgesellschaft, Weinheim, 1986

siehe auch
DOSE E.: Thoughts on photomeric precision and accuracy
			SocAstSci Proceedings 37, S. 63 , 2018